Game
Theory: An Introductory Sketch
|
|
Some
Examples of Games with More Complex Structures
All of the game examples so far are relatively simple in that time plays no part in them, however complex they may be in other ways. The passage of time can make at least three kinds of differences. First, people may learn -- new information may become available, that affects the payoffs their strategies can give. Second, even when people do not or cannot commit themselves at first, they may commit themselves later -- and they may have to decide when and if to commit. Of course, this blurs the distinction we have so carefully set up between cooperative and noncooperative games, but life is like that. Third, there is the possibility of retaliation against other players who fail to cooperate with us. That, too, blurs the cooperative-noncooperative distinction. That means, in particular, that repeated games -- and particularly repeated prisoners' dilemmas -- may have quite different outcomes than they do when they are played one-off. But we shall leave the repeated games out as an advanced topic and move on to study sequential games and the problems that arise when people can make commitments only in stages, at different points in the game. I personally find these examples interesting and to the point and they are somewhat original.
There are some surprising results. One surprising result is that, in some games, people are better off if they can give up some of their freedom of choice, binding themselves to do things at a later stage in the came that may not look right when they get to this stage. An example of this (I suggest) is to be found in Marriage Vows. This provides a good example of what some folks call "economic imperialism" -- the use of economics (and game theory) to explain human behavior we do not usually think of as economic, rational, or calculating -- although you do not really need to know any economics to follow the example in Marriage Vows. Another example along the same line (although the main application is economics in a more conventional sense) is The Paradox of Benevolent Authority, which tries to capture, in game-theoretic terms, a reason why liberal societies often try to constrain their authorities rather than relying on their benevolence.
Also, the following example will have to do with relations between an employer and an employee: A Theory of Burnout. For an example in which flexibility is important, so that giving up freedom of choice is a bad idea, and another non-imperialistic economic application of game theory, see The Essence of Bankruptcy. Of course, that note is meant to discuss bankruptcy, not to exemplify it!
Game
Theory: An Introductory Sketch
A
Theory of Marriage Vows
This example is an attempt to use game theory to "explain" marriage vows. But first (given the nature of the topic) it might be a good idea to say something about "explanation" using game theory.
One possible objection is that marriage is a very emotional and even spiritual topic, and game theory doesn't say anything about emotions and spirit. Instead game theory is about payoffs and strategies and rationality. That's true, but it may be that the specific phenomenon -- the taking of vows that (in some societies, at least) restrict freedom of choice -- may have more to do with payoffs and strategies than with anything else, and may be rational. In that case, a game-theoretic model may capture the aspects that are most relevant to the institution of marriage vows. Second, game-theoretic explanations are never conclusive. The most we can say is that we have a game-theoretic model, with payoffs and strategies like this, that would lead rational players to choose the strategies that, in the actual world, they seem to choose. It remains possible that their real reasons are different and deeper, or irrational and emotional. That's no less true of bankruptcy than of marriage. Indeed, from some points of view, their "real reasons" have to be deeper and more complex -- no picture of the world is ever "complete." The best we can hope for is a picture that fits fairly well and contains some insight. I think game theory can "explain" marriage vows in this sense.
In some sequential games, in which the players have to make decisions in sequence, freedom of choice can be a problem. These are games that give one or more players possibilities for "opportunism." That is, some players are able to make their decisions in late stages of the game in ways that exploit the decisions made by others in early stages. But those who make the decisions in the early stages will then avoid decisions that make them vulnerable to opportunism, with results that can be inferior all around. In these circumstances, the potential opportunist might welcome some sort of restraint that would make it impossible for him to act opportunistically at the later stage. Jon Elster made the legend of "Ulysses and the Sirens" a symbol for this. Recall, in the legend, Ulysses wanted to hear the sirens sing; but he knew that a person who would hear them would destroy himself trying to go to the sirens. Thus, Ulysses decided at the first stage of the game to have himself bound to the mast, so that, at the second stage, he would not have the freedom to choose self-destruction. Sequential games are a bit different from that, in that they involve interactions of two or more people, but the games of sequential commitment can give players reason to act as Ulysses did -- that is, to rationally choose at the first step in a way that would limit their freedom of choice at the second step. That is our strategy in attempting to "explain" marriage vows.
Here is the "game." At the first stage, two people get together. They can either stay together for one period or two. If they take a vow, they are committed to stay together for both periods. During the first period, each person can choose whether or not to "invest in the relationship." "Investing in the relationship" means making a special effort in the first period that will only yield the investor benefits in the second period, and will yield benefits in the second period only if the couple stay together. At the end of the first period, if there has been no vow, each partner decides whether to remain together for the second period or separate. If either prefers to separate, then separation occurs; but if both choose to remain together, they remain together for the second period. Payoffs in the second period depend on whether the couple separate, and, if they stay together, on who invested in the first period.
The payoffs are determined as follows: First, in the first stage, the payoff to one partner is 40, minus 30 if that partner "invests in the relationship," plus 20 if the other partner "invests in the relationship." Thus, investment in the relationship is a loss in the first period -- that's what makes it "investment." In the second period, if they separate, both partners get additional payoffs of 30. Thus, each partner can assure himself or herself of 70 by not investing and then separating. However, if they stay together, each partner gets an additional payoff of 20 plus (if only the other partner invested) 25 or (if both partners invested) 60.
Notice that the total return to investment to the couple over both periods is disproportionately greater if both persons invest -- that is, it is 2*20-2*30 in the first period plus 2*60 = 80 if both invest, but is 20-30+25=15 if only one invests. The difference 80-2*15=50 reflects the assumption that the investments are complementary -- that each partner's investment reinforces and increases the productivity of the other person's investment.
These ground rules lead to the payoffs in Table 15-1, in which "his" payoffs are to the right in each pair and "hers" are to the left.
Table 15-1
|
|
him |
|||
|
her |
invest |
don't invest |
||
|
invest/ |
stay |
separate |
stay |
separate |
|
stay |
110, 110 |
60, 60 |
30, 105 |
40, 115 |
|
separate |
60, 60 |
60, 60 |
40, 115 |
40, 115 |
|
don't invest/ |
|
|
|
|
|
stay |
105, 30 |
115, 40 |
60, 60 |
70, 70 |
|
separate |
115, 40 |
115, 40 |
70, 70 |
70, 70 |
Since the decision to invest (or not) precedes the decision to separate (or not) we have to work backward to solve this game. Suppose that there are no vows and both partners invest. Then we have the subgame in the upper left quarter of the table:
|
110, 110 |
60, 60 |
|
60, 60 |
60, 60 |
Clearly, in this subgame, to remain together is a dominant strategy for both partners, so we can identify 110, 110 as the payoffs that will in fact occur in case both partners invest.
Now take the other symmetrical case and suppose that neither partner invests. We then have the subgame at the lower right:
|
60, 60 |
70, 70 |
|
70, 70 |
70, 70 |
Here, again, we have a clear dominant strategy, and it is to separate. The payoffs of symmetrical non-investment are thus 70,70.
Now suppose that only one partner invests, and (purely for illustrative purposes!) we consider the case in which "he" invests and "she" does not. We then have the subgame at the lower right:
|
105, 30 |
115, 40 |
|
115, 40 |
115, 40 |
Here again, separation is a dominant strategy, so the payoffs for the subgame where "she" invests and "he" does not are 115,40. A symmetrical analysis will give us payoffs of 40, 115 when "she" invests and "he" does not.
Putting these subgame outcomes together in a payoff table for the decision to invest or not invest we have:
Table 15-2
|
|
he |
|
|
|
invest |
don't invest |
|
she |
|
|
|
invest |
110, 110 |
40, 115 |
|
don't invest |
115, 40 |
70, 70 |
This game resembles the Prisoners' Dilemma, in that non-investment is a dominant strategy, but when both players play their dominant strategies, both are worse off than they would be if both played the non-dominant strategy. Anyway, we identify 70, 70 as the subgame perfect equilibrium in the absence of marriage vows.
But now suppose that, back at the beginning of things, the pair have the option to take, or not to take, a vow to stay together regardless. If they take the vow, only the "stay together" payoffs would remain as possibilities. If they do not take the vow, we know that there will be a separation and no investment, so we need consider only that possibility. In effect, there are three strategies: take a vow and invest, take a vow and don't invest, or don't take a vow. We have
Table 15-3
|
|
he |
||
|
|
vow & invest |
vow & don't invest |
don't vow |
|
she |
|
|
|
|
vow & invest |
110, 110 |
30, 105 |
70, 70 |
|
vow & don't invest |
105, 30 |
60, 60 |
70, 70 |
|
don't vow |
70, 70 |
70, 70 |
70, 70 |
In this game, there is no dominant strategy. However, the only Nash equilibrium is for each player to take the vow and invest, and thus the payoff that will occur if a vow can be taken is at the upper left -- 110, 110, the "efficient" outcome. In effect, willingness to take the vow is a "signal" that the partner intends to invest in the relationship -- if (s)he didn't, it would make more sense for him (her) to avoid the vow. Both partners are better off if the vow is taken, and if they had no opportunity to bind themselves with a vow, they could not attain the blissful outcome at the upper left.
Thus, when each partner decides whether or not to take the vow, each rationally expects a payoff of 110 if the vow is taken and 70 if not, and so, the rational thing to do is to take the vow. Of course, this depends strictly on the credibility of the commitment. In a world in which marriage vows become of questionable credibility, this reasoning breaks down, and we are back at Table 2, the Prisoners' Dilemma of "investment in the relationship." Some sort of first-stage commitment is necessary. Perhaps emotional commitment will be enough to make the partnership permanent -- emotional commitment is one of the things that is missing from this example. But emotional commitment is hard to judge. One of the things a credible vow does is to signal emotional commitment. If there are no vows that bind, how can emotional commitment be signaled? That seems to be one of the hard problems of living in modern society!
There is a lot of common sense here that your mother might have told you -- anyway my mother would have! What the game-theoretic analysis gives us is an insight on why Mom was right, after all, and how superficial reasoning can mislead us. As we compare tables 2 and 3, we can observe that -- given the choices made, that is, reading down a column or across a row -- no-one is ever better off with Table 3 (vow) than with Table 2 (no vow). And except for the upper left quadrant, both parties are worse off with the vow than without it. Thus I might reason -- wrongly! -- that since, ceteris paribus, I am better off with freedom of choice than without it, I had best not take the vow. But this illustrates a pitfall of "ceteris paribus" reasoning. In this comparison, ceteris are not paribus. Rather, the outcomes of the various subgames -- "ceteris" -- depend on the payoff possibilities as a whole. The vow changes the whole set of payoff possibilities in such a way that "ceteris" are changed -- non paribus -- and the outcome improved. The set of possible outcomes is worse but the selection of outcomes among the available set is so much improved that both parties are almost twice as well off as they would be had they not agreed to restrain their freedom of choice.
In other words: Cent' Anni!
The
Paradox of Benevolent Authority
The "Prisoners' Dilemma" is without doubt the most influential single analysis in Game Theory, and many social scientists, philosophers and mathematicians have used it as a justification for interventions by governments and other authorities to limit individual choice. After all, in the Prisoners' Dilemma, rational self-interested individual choice makes both parties worse off. A difficulty with this sort of reasoning is that it treats the authority as a deus ex machina -- a sort of predictable, benevolent robot who steps in and makes everything right. But a few game theorists and some economists (influenced by Game Theory but not strictly working in the Game Theoretic framework) have pointed out that the authority is a player in the game, and that makes a difference. This essay will follow that line of thought in an explicitly Game-Theoretic (but very simple) frame, beginning with the Prisoners' Dilemma. Since we begin with a Prisoners' Dilemma, we have two participants, whom we will call "commoners," who interact in a Prisoners' Dilemma with payoffs as follows:
Table 16-1
|
|
|
Commoner 1 |
|
|
|
|
cooperate |
defect |
|
Commoner 2 |
cooperate |
10,10 |
0,15 |
|
defect |
15,0 |
5,5 |
|
The third player in this game is the "authority," and she (or he) is a very strange sort of player. She can change the payoffs to the commoners. The authority has two strategies, "penalize" or "don't penalize." If she chooses "penalize," the payoffs to the two commoners are reduced by 7. If she chooses "don't penalize," there is no change in the payoffs to the two commoners.
The authority also has two other peculiar characteristics:
- She is benevolent: the payoff to the authority is the sum of the payoffs to the commoners.
- She is flexible: the authority chooses her strategy only after the commoners have chosen theirs.
Now suppose that the authority chooses the strategy "penalize" if, and only if, one or both of the commoners chooses the strategy "defect." The payoffs to the commoners would then be
Table 16-2
|
|
|
Commoner 1 |
|
|
|
|
cooperate |
defect |
|
Commoner 2 |
cooperate |
10,10 |
-7,8 |
|
defect |
8,-7 |
-2,-2 |
|
But the difficulty is that this does not allow for the authority's flexibility and benevolence. Is that indeed the strategy the authority will choose? The strategy choices are shown as a tree in Figure 1 below. In the diagram, we assume that commoner 1 chooses first and commoner 2 second. In a Prisoners' Dilemma, it doesn't matter which participant chooses first, or they both choose at the same time. What is important is that the authority chooses last.

Figure 16-1
What we see in the figure is that the authority has a dominant strategy: not to penalize. No matter what the two commoners choose, imposing a penalty will make them worse off, and since the authority is benevolent -- she "feels their pain," her payoffs being the sum total of theirs -- she will always have an incentive to let them off, not to penalize. But the result is that she cannot change the Prisoners Dilemma. Both commoners will choose "defect," the payoffs will be (5,5) for the commoners, and 10 for the authority.
Perhaps the authority will announce that she intends to punish the commoners if they choose "defect." But they will not be fooled, because they know that, whatever they do, punishment will reduce the payoff to the authority herself, and that she will not choose a strategy that reduces her payoffs. Her announcements that she intends to punish will not be credible.
EXERCISE In this example, a punishment must fall on both commoners, even if only one defects. Does this make a difference for the result? Assume instead that the authority can impose a penalty on one and not the other, so that the authority has 4 strategies: no penalty, penalize commoner 1, penalize commoner 2, penalize both. What are the payoffs to the authority in the sixteen possible outcomes that we now have? Under what circumstances will a benevolent authority penalize? What are the equilibrium outcomes in this more complicated game?
There are two ways to solve this problem. First, the authority might not be benevolent. Second, the authority might not be flexible.
Non-benevolent authority:
We might change the payoffs to the authority so that the authority no longer "feels the pain" of the commoners. For example, make the payoff to the authority 1 if both commoners cooperate and zero otherwise. We might call an authority with a payoff system like this a "Prussian" authority, since she values "order" regardless of the consequences for the people, an attitude sometimes associated with the Prussian state. She then has nothing to lose by penalizing the commoners whenever there is defection, and announcements that she will penalize defection become credible. EXERCISE Suppose the authority is sadistic; that is, the authority's payoff is 1 if a penalty is imposed and 0 otherwise. What will be the game equilibrium in this case?
Non-flexible authority:
If the authority can somehow commit herself to imposing the penalty in some cases and not in others, perhaps by posting a bond greater than the 15 point cost of a penalty, then the announcement of an intention to penalize would become credible. The announcement and commitment would then be a strategy choice that the authority would make first, rather than last. Let's say that at the first step, the authority has two strategies: commit to a penalty whenever any commoner chooses "defect," or don't commit. We then have a tree diagram like Figure 2. What we see in Figure 2 is that if the authority commits, the outcome will be cooperation and a payoff of 20 for her, at the top; but if she does not commit, the outcome will be at the bottom -- both commoners defect and the payoff will be -4 for the authority. So the authority will choose the strategy of commitment, if she can, and in that case the rational, self-interested action of the commoners will lead to cooperation and good results. But, if the commoners irrationally defect, or if they don't believe the commitment and defect for that reason, then the authority is boxed in. She has to impose a penalty even though it makes everyone worse off. In short, she cannot be flexible.
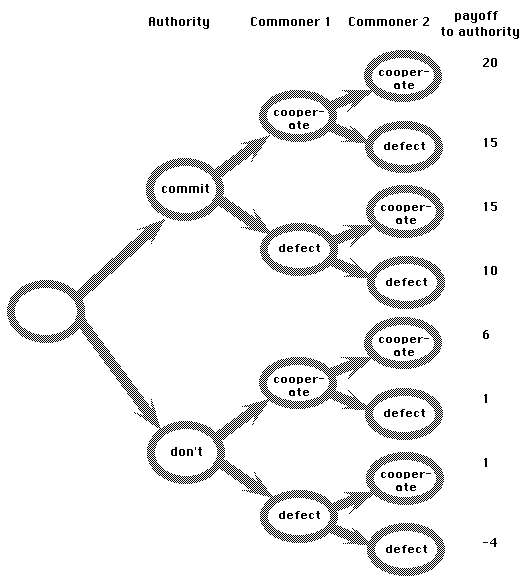
Figure 16-2
What we have seen here are two principles that play an important part in modern macroeconomics. Many modern economists apply these principles to the central banks that control the money supply in modern economies. They are
The principle of "rules rather than discretion."
That is, the authority should act according to rules chosen in advance, rather than responding flexibly to events as they occur. In the case of the central banks, they should control the money supply or the interest rate on public debt (there is controversy about which) according to some simple rule, such as increasing the money supply at a steady rate or raising the interest rate when production is close to capacity, to prevent inflation. If some groups in the economy push their prices up, the monetary authority might be tempted to print money, which would cause inflation and help other groups to catch up with their prices, and perhaps reduce unemployment. But this must be avoided, since the groups will come to anticipate it and just push their prices up all the faster.
The principle of credibility.
It is not enough for the authority to be committed to the simple rule. The commitment must be credible if the rule is to have its best effect.
The difficulty is that it may be difficult for the authority to commit itself and to make the commitment credible. This can be illustrated by another application: dealing with terrorism. Some governments have taken the position that they will not negotiate with terrorists who take hostages, but when the terrorists actually have hostages, the pressure to make some sort of a deal can be very strong. What is to prevent a sensitive government from caving in -- just this once, of course! And potential terrorists know those pressures exist, so that the commitments of governments may not be credible to them, even when the governments have a "track record" of being tough.
This may have an effect on the way we want our institutions to function, at the most basic, more or less constitutional level. For example, in countries with strong currencies, like Germany and the United States, the central bank or monetary authority is strongly insulated from democratic politics. This means that the pressures for a more "flexible" policy expressed by voters are not transmitted to the monetary authority -- or, anyway, they are not as strong as they might otherwise be -- so the monetary authority is more likely to commit itself to a simple rule and the commitment will be more credible.
Are these "conservative" or "liberal" ideas? Some would say that they are conservative rather than liberal, on the grounds that liberals believe in flexibility -- considering each case on its own merits, and making the best decision in the circumstances, regardless of unthinking rules. But it may be a little more complex than that. This and the previous essay have considered particular cases in which commitment and rules work better than flexibility. There may be many other cases in which flexibility is needed. I should think that the "liberal" approach would be to consider the case for commitment and for rules rather than discretion on its merits in each instance, rather than relying on an unthinking rule against rules! Anyway, conservative or liberal or radical (as it could be!), the theory of games in extended form is now a key tool for understanding the role of commitment and rules in any society.
A
Theory of Burnout
As an illustration of the concepts of sequential games and subgame perfect equilibrium, we shall consider a case in the employment relationship. This game will be a little richer in possibilities than the economics textbook discussion of the supply and demand for labor, in that we will allow for two dimensions of work the principles course does not consider: variable effort and the emotional satisfactions of "meaningful work." We also allow for a sequence of more or less reliable commitments in the choice of strategies.
We consider a three-stage game. At the first stage, one player in the game, the "worker," must choose between two kinds of strategies, that is, two "jobs." In either job, the worker will later have to choose between two rates of effort, "high" and "low." In either job, the output is 20 in the case of high effort and 10 if effort is low. We suppose that the first job is a "meaningful job," in the sense that it meets needs with which the worker sympathizes. As a consequence of this, the worker "feels the pain" of unmet needs when her or his output falls below the potential output of 20. This reduces her or his utility payoff when she or he shirks at the lower effort level. Of course, her or his utility also depends on the wage and (negatively) on effort. Accordingly, in Job 1 the worker's payoff is
wage - 0.3(20-output) - 2(effort) where effort is zero or one. The other job is "meaningless," so that the worker's utility does not depend on output, and in this job it is wage - 2(effort)
At the second stage of the game the other player, the "employer," makes a commitment to pay a wage of either 10 or 15. Finally, the worker chooses an effort level, either 0 or 1.
The payoffs are shown in Table 17-1.
Table 17-1
|
|
|
|
Job |
|||
|
|
|
|
1 |
2 |
||
|
|
|
effort |
0 |
1 |
0 |
1 |
|
wage |
high |
|
-5, 12 |
5, 13 |
-5,15 |
5,13 |
|
low |
|
0,7 |
10,8 |
0,10 |
10,8 |
|
In each cell of the matrix, the worker's payoff is to the right of the comma and the employer's to the left. Let us first see what is "efficient" here. The payoffs are shown in Figure 1. Payoffs to the employer are on the vertical axis and those to the worker on the horizontal axis. Possible payoff pairs are indicated by stars-of-David. In economics, a payoff pair is said to be "efficient," or equivalently, "Pareto-optimal," if it is not possible to make one player better off without making the other player worse off. The pairs labeled A, B, and C have that property. They are (10,8), (5,13) and (-5,15). The others are inefficient. The red line linking A, B, and C is called the utility possibility frontier. Any pairs to the left of and below it are inefficient.

Figure
17-1: Game Outcomes
Now let us explore the subgame perfect equilibrium of this model. First, we may see that the low wage is a "dominant strategy" for the employer. That is, regardless which strategy the worker chooses -- job 1 and low effort, job 2 and high effort, and so on -- the employer is better off with low wages than with high. Thus the worker can anticipate that the wages will be low. Let us work backward. Suppose that the worker chooses job 2 at the first stage. This limits the game to the right-hand side of the table, which has a structure very much like the Prisoners' Dilemma. In this subgame, both players have dominant strategies. The worker's dominant strategy is low effort, and the Prisoners' Dilemma-like outcome is at (0,10). This is the outcome the worker must anticipate if he chooses Job 2.
What if he chooses Job 1? Then the game is limited to the left-hand side. In this game, too, the worker, like the employer, has a dominant strategy, but in this case it is high effort. This subgame is not Prisoners' Dilemma-like, since the equilibrium -- (10,8) -- is an efficient one. This is the outcome the worker must expect if she or he chooses Job 1, "meaningful work."
But the worker is better off in the subgame defined by "nonmeaningful work," Job 2. Accordingly, she will choose Job 2, and thus the equilibrium of the game as a whole (the subgame perfect equilibrium) is at (0,10). It is indicated by point E in the figure, and is inefficient.
Why is meaningful work not chosen in this model? It is not chosen because there is no effective reward for effort. With meaningful work, the worker can make no higher wage, despite her greater effort. Yet she does not reduce her effort because doing so brings the greater utility loss of seeing the output of meaningful work decline on account of her decision. The dilemma of having to choose between a financially unrewarded extra effort and witnessing human suffering on account of one's failure to make the effort seems to be a very stylized account of what we know as "burnout" in the human service professions.
Put differently, workers do not choose meaningful work at low wages because they have a preferable alternative: shirking at low effort levels in nonmeaningful jobs. Unless the meaningful jobs pay enough to make those jobs, with their high effort levels, preferable to the shirking alternative, no-one will choose them.
Inefficiency in Nash equilibria is a consequence of their noncooperative nature, that is, of the inability of the players to commit themselves to efficiently coordinated strategies. Suppose they could do so -- what then? Suppose, in particular, that the employer could commit herself or himself, at the outset, to pay a high wage, in return for the worker's commitment to choose Job 1. There is no need for an agreement about effort -- of the remaining outcomes, in the upper left corner of the table, the worker will choose high effort and (5,13), because of the "meaningful" nature of the work. This is an efficient outcome.
And that, after all, is the way markets work, isn't it? Workers and employers make reciprocal commitments that balance the advantages to one against the advantages to the other? It is, of course, but there is an ambiguity here about time. There is, of course, no measurement of time in the game example. But commitments to careers are lifetime commitments, and correspondingly, the wage incomes we are talking about must be lifetime incomes. The question then becomes, can employers make credible commitments to pay high lifetime income to workers who choose "meaningful" work with its implicit high effort levels? In the 1960's, it may have seemed so; but in 1995 it seems difficult to believe that the competitive pressures of a profit-oriented economic system will permit employers to make any such credible commitments.
This may be one reason why "meaningful work" has generally been organized through nonprofit agencies. But under present political and economic conditions, even those agencies may be unable to make credible commitments of incomes that can make the worker as well off in a high-effort meaningful job as in a low-effort nonmeaningful one. If this is so, there may be little long-term hope for meaningful work in an economy dominated by the profit system.
Lest I be misunderstood, I do not mean to argue that a state-organized system would do any better. There is an alternative: a system in which worker incomes are among the objectives of enterprises, that is, a cooperative system. It appears to be possible that such a system could generate meaningful work. There is empirical evidence that cooperative enterprises do in fact support higher effort levels than either profit-oriented or state organizations.
Of course, some nonmeaningful work has to be done, and it remains true that when nonmeaningful work is done it is done inefficiently and at a low effort level, that is, at E in the figure. In other words, the fundamental source of inefficiency in this model is the inability of the workers to make a credible commitment to high effort levels. If high effort could somehow be assured, then (depending on bargaining power) a high-effort efficient outcome would become a possibility in the nonmeaningful work subgame, and this in turn would eliminate the worker's incentive to choose nonmeaningful work in order to shirk. (If worker bargaining power should enforce the outcome at C, which is Pareto-optimal, the shirking nonmeaningful strategy would still dominate meaningful work). However, it does seem that it is very difficult to make commitments to high effort levels credible, or enforceable, in the context of profit-oriented enterprises.
It may be, then, the the problem of finding meaningful work and of burn-out in fields of meaningful work is a relatively minor aspect of the far broader question of effort commitment in modern economic systems. Perhaps it will do nevertheless as an example of the application of subgame perfect equilibrium concepts to an issue of considerable interest to many modern university students.
Game
Theory: An Introductory Sketch
The
Essence of Bankruptcy
Bankruptcy is badly understood in modern economics. This is equally true at the most elementary and most advanced levels, but, of course, the sources of confusion are different in these different contexts.
For the elementary student, there is the tendency to confuse bankruptcy, the decision to shut down production, and "going out of business," that is, liquidation. The undergraduate textbook encourages this, since it considers only the shut-down decision, and the timeless model usual in the undergraduate textbook makes the shut-down decision appear to be an irreversible one. The textbook discussion of the shut-down observes that the business will shut down if it cannot cover its variable costs, and this illustrates a point about opportunity costs -- fixed costs are not considered because they are not opportunity costs in the short run. Bankruptcy occurs when the firm cannot, or will not, cover its debt service payments: quite a different thing. Debt service costs are usually thought of as fixed, not variable costs.
In real businesses, of course, bankruptcy, liquidation, and shut-down are three quite different things that may appear in various combinations or entirely separately. A business may be reorganized under bankruptcy and continue doing business with the former creditors as equity owners -- neither shut down nor liquidated. The business that shuts down may not be bankrupt -- it may continue to make debt service payments out of its cash reserves and resume production when conditions merit. And a company may be liquidated, for example at the death of a proprietor, although it is able to cover its variable costs and its debt service payments (although this will only occur when the transaction costs of finding a buyer are so high as to make sale of the business infeasible).
Small wonder, then, that the undergraduate economics student finds the shut-down analysis a little confusing -- it abstracts from almost everything that matters! But more advanced economists will find bankruptcy confusing for another reason. The reason is related to the phrase "the firm cannot, or will not, cover its debt service payments." We may think of a lending agreement as a solution to a cooperative game, that is, a game in which both players commit themselves at the outset to coordinated strategies. The repayment of debt service is the strategy the firm has committed itself do. For the firm to fail to pay its debt service contradicts the supposition that the firm had, at the first instance, committed itself. And the creditors are letting the firm out of its contract, and they are losing by that, and why should they do it? It seems that we must fall back on the first part of the statement: the firm cannot make its debt service payments. Some unavoidable (but not clearly foreseen) circumstance makes it impossible for the debt service to be paid. We then interpret the debt contract as a commitment to pay "if possible," or with some other such weasel-words, and we understand why the creditor capitulates: she or he has no choice.
But how can it be that "the firm cannot" pay its debt service? We need to make our picture a little more detailed.
First, uncertainty clearly plays a part in it. If bankruptcy were certain, there would be no lending. Accordingly, we represent uncertainty in the usual way in modern economics: we suppose that the world may realize one of two or more states. At the outset, the state of the world is not known. After some decisions and commitments are made, the state of the world is revealed, and some of the decisions and commitments made at the first stage must be reconsidered. Bankruptcy is such a reconsideration of commitments made in ignorance of the state of the world: it occurs only in some states of the world, and the payoff to the lender in the other states is good enough to make the deal acceptable as a whole.
Second, we must be a little more careful about just who "the firm" is, since it is a compound player. Let us adopt the John Bates Clark model of the business enterprise, and of the market economy, as a first approximation. In this model there are capitalists (lenders, for our purposes), suppliers of labor services, that is workers, and "the entrepreneur," who owns nothing and whose services are those of coordination between the other two groups.
With these specifics in mind, let us return to the shut-down decision as it is portrayed in the intermediate microeconomics text. What leads "the firm" to shut down? What happens is that the state of the world realized is a relatively bad one. That is, the conditions for production and/or demand are poor, so that the enterprise is unable to "cover its variable costs." In other words, it is unable to pay the workers enough to keep them in the enterprise. The key point here is that the workers have alternatives. The revenue of the enterprise is so little that, even if the workers get it all, they do not make as much as they would in their best alternatives. Saying "the firm cannot cover its variable costs" is a coded way of saying "the firm cannot recruit labor with its available revenues." In such a case, there is clearly no alternative to shutting down.
But, as we have observed, a firm may go bankrupt but not shut down, instead continuing to produce under reorganized ownership. How would this occur? The state of the world is not quite as bad: the enterprise can earn enough revenue to pay its workers their best alternative wages, but having done that, there is not enough left to pay the debt service. The entrepreneur has only two choices: to cut the wages below the workers' best alternative pay, lose them all, produce nothing, and default on all of the debt service; or to pay the workers at their best alternative, produce something, and pay something toward the debt service. Clearly, the latter is in the interest of the lenders, so they renegotiate the note.1
In all of this, "the entrepreneur" has played a passive role. John Bates Clark's "entrepreneur" is not much of a player, from the point of view of game theory, anyway. His role is to combine capital and labor in such a way as to maximize profits. In effect, he is an automaton whose programmed decisions define the rules of a game between the workers and the bankers. At the point of bankruptcy, his role is even less active. The choices and commitments are made by the substantive players: capitalists and workers. The essence of bankruptcy is a game played between a lender and a group of workers. We may as well eliminate the entrepreneur entirely, and think of the firm as a worker-cooperative.2 From here on, we shall follow that strategy.
To make things more explicit still, let us consider a numerical example. The players are, as before, a banker and a group of workers. If the banker lends and the workers work, the enterprise can produce a revenue that depends on the state of the world. there are three states. The best state is the "normal" one, so we assign it a probability of 0.9. The other two states are bad and worse -- a bankruptcy state and a shut-down state -- with probabilities of 0.05 each. Thus production possibilities are as shown in Table 18-1.
Table
18-1
|
state |
revenue |
probability |
|
1 |
3000 |
0.9 |
|
2 |
2000 |
0.05 |
|
3 |
1000 |
0.05 |
We suppose that the safe rate of return (opportunity cost of capital) is .01, and that the lender, being profit oriented, offers a loan of 1000 to enable production to take place. The contract rate of interest is 10%; i.e. 1100 has to be paid back at the end of the period. We suppose, also, that the workers can get an alternative pay amounting to 1500.
If the loan is made, the state of the world is revealed, and then the participants reconsider their strategy choices in the light of the new information. Should the bank make the loan? Should the workers' cooperative accept it? We shall have to consider the various outcomes and then apply "backward induction" to get the answer.
What then happens in state 3? The answer is that in state 3, the members of the cooperative all resign in order to take their best alternative opportunities, at 1500>1000, so that the cooperative spontaneously ceases to exist, and the lender gets nothing.
What about state 1? The enterprise revenue is enough to pay the 1100 in debt service, and the workers' income, 1900, is more than their best alternative, so they do stay and produce, and both the bank and the workers' cooperative are better off.
We now turn to the pivotal state 2. Here, there is enough revenue to pay the debt service, but if it is paid, the workers get only 900<1500. In such a case, again, the worker-members of the cooperative will resign, and the cooperative dissolve for lack of members, and the bank will get nothing. On the other hand, if the bank renegotiates for partial repayment of 500 or less, then the workers get 1500 and the cooperative continues. Thus, in this state, the bank renegotiates and earns 500.
The bank's expected repayment thus is
.9(1100) + .05(500) + .05(0) = 1015 > 1010
Thus the bank makes more than its best alternative and will accept the contract. As for the workers in the cooperative, they make a mathematical expectation of
.9(1900) + .05(1500) + .05(1500) = 1860 > 1500
And so they, too, accept the contract. Thus the loan is made, despite a .05 probability of bankruptcy and a .05 probability of outright default.
In many games of this kind one or another player can obtain a better result if he can commit himself credibly at the outset to a strategy which may seem less advantageous, once the state of the world is known and others have made their decisions. Would the bank be better off it if could commit itself not to renegotiate? The answer is that it would not. Its payoffs would be
.9(1100) + .05(0) + .05(0) = 990 < 1010
The lenders would be worse off and, if (for example) statute law forbade them from renegotiating, they would refuse to make the loan!
But what about the workers? It is their desertion that leads the enterprise to be abandoned if the debt service is paid in state 2. What if they could be somehow bound to the firm? Slavery offers one possibility. In a system that permits slavery, "the entrepreneur" might buy slaves instead of hiring free workers. In state of nature 3, "the entrepreneur" would rent out the slave work force for 1500, pay the 1100 debt service, and pocket the profits (assuming the cost of food necessary to keep the slaves productive is less than 400). In state 2, "the entrepreneur" would require the slaves to work in the firm, produce 2000, pay the debt service, and pocket 900 less the cost of their food. The bank would get its debt service in every state (barring slave starvation) and might well prefer to lend to slavemasters rather than worker cooperatives or John Bates Clark style firms.
In the context of the John Bates Clark firm, the desertion of the workers in states 2 and 3 comes as no surprise to us -- the workers are hired by "the entrepreneur" at mutual convenience and are expected to leave whenever it benefits them to do so. In this example, however, the loan is made to a cooperative association of the workers, their own association. If it were made to them individually, they would be no less responsible for it after they had moved on to their other, better-paying jobs. But the obligation to pay the loan has been assumed by a group of workers, as a group, and the group can continue to exist only so long as it is in the interest of the workers as individuals for it to do so. And this does not reflect the constitution of the firm, but the liberal constitution of society, that holds that no agency, even one constructed by the workers, may require a person to work without offering a payment sufficient to get the worker's assent.
And this is the essence of the case for the proprietary or corporate enterprise as well. The proprietor or investor-owned corporation is no more than a middleman between a group of workers and a bank, so far as bankruptcy is concerned. The essence of bankruptcy is a renegotiation of the loan contract between a lender and a group of workers, and laws exempting the creditor from the full amount of the debt, in appropriate circumstances, are laws for the protection of the creditors, not of the debtors.
****************************************************************************************************************
|
Auction Types -
Standard |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
Here are the types of auctions you will encounter on this site.
|
||||||||||||||||||||||||||||||
|
*****************“The Bidding Game” was written by science writer Erica Klarreich************************ ***************Auction ****************** What exactly is an
auction? You've seen auctions in movies, you've read about them, you've
probably participated and believe nothing could be more simple, right?
Someone bids, the price goes up, someone else bids, and when everyone is
silent, the object is sold. Well . . . sometimes. More to the point, why does it matter? Perhaps because auctions are a
multi-billion dollar business, and the mortgage rate you pay is determined in
part by auctions held by the U.S. Treasury. Perhaps because that particular
auction is not the kind of auction you think it is. Perhaps because some
bidders spend years mastering strategies that enable them to exploit the
misunderstandings of the unwary. And perhaps because smart auction principles
can be used to buy and sell computer resources in a way that substantially
optimizes human time and money. However, before all that, what exactly is an
auction? Even the term auction (root, "auctio", means increase) is a
misnomer because not all auctions have ascending price schemes. In fact,
there are many different auction formats including the familiar ascending
bid, but also including the descending, sealed-bid, simultaneous, handshake,
and whispered forms of bidding. Many of the more unusual formats have been
practiced for hundreds of years including one variety in which huge estates
have been sold during the time it took for a single one-inch candle stub to
flicker out. Auctions are useful when selling a commodity of undetermined quality.
Banks compete for loan customers of uncertain risk, graduate schools compete
for students of unknown ability, [Vincent]
wine merchants may not have tasted the wares. Auctions can be used for single
items such as a work of art and for multiple units of a homogeneous item such
as gold or Treasury securities. For countries changing from centrally-planned
to market-based economies, auctions offer an ability to value goods that might
not otherwise be available. They are useful in circumstances wherein the
goods do not have a fixed or determined market value, in other words, when a
seller is unsure of the price he can get. Choosing to sell an item by auctioning it off is more flexible than
setting a fixed price and less time-consuming and expensive than negotiating
a price (such as happens in a car lot). In a price negotiation, each bid and
counter-bid is considered separately, but in an auction the competing bids
are offered almost simultaneously. In fact, an auctionable resource can be nearly anything--public land,
livestock, wine, flowers, fish, cars, construction contracts, equity shares,
or contracts in the game of bridge. The common denominator is that the value
of each item varies enough to preclude direct and absolute pricing. In one
fascinating experiment, external offices (with prized windows and locations)
were auctioned off as a way of solving the quandary of how to allocate
physical resources at Arizona State University's College of Business without
infuriating the entire staff. [Boyes]
Simply stated, an auction is a method of allocating scarce goods, a method
that is based upon competition. It is the purest of markets: a seller wishes
to obtain as much money as possible, and a buyer wants to pay as little as
necessary. An auction offers the advantage of simplicity in determining
market-based prices. It is efficient in the sense that an auction usually
ensures that resources accrue to those who value them most highly and ensures
also that sellers receive the collective assessment of the value. (In later
chapters, we will see that sellers do not necessarily receive maximum value
in the ascending-bid format. [Varian])
What is unique about the auction is that the price is set not by the seller,
but by the bidders. On the other hand, it is the seller who sets the rules by choosing the
type of auction to be used. One oddity regularly occurs in the wine auction market. [Ashenfelter]
It is commonly understood in wine circles that when identical lots of wine
are peddled at the same auction, later lots are frequently sold for a lower
price than early lots. Auctioneers know this but are reluctant to reveal this
information to inexperienced participants because such bidders often conclude
that the auction house is dishonest. Thus, auctioneers have learned to
disguise this anomaly by offering small lots of wine A before offering larger
lots of wine A. People assume the reason for the price difference comes from
a quantity discount, and so they pay no attention. In fact, the difference is
real. An auction is unusual also in that, unlike other methods of selling,
generally the auctioneer doesn't own the goods, but acts rather, as an agent
for someone who does. Frequently, the buyers know more than the seller about
the value of the item. A seller, not wanting to suggest a price first out of
fear that his ignorance will prove costly, holds an auction to extract
information he might not otherwise realize. There are different ways to classify auctions. There are open auctions as
well as sealed-bid auctions. There are auctions where the price ascends and
auctions where the price drops at regular intervals. Generally, experts agree
that there are four major one-sided
auction formats: English, Dutch, First-Price sealed-bid, and Vickrey
(uniform second-price). One difficulty is the lack of commonality in naming
conventions. What some people call a uniform second-price auction is known in
financial communities as a Dutch auction, and no end of confusion results. Which auction is best? The answer depends upon many variables. A seller's
perspective is different from that of a buyer. Some auctions types decrease
the incentives to cheat while others provide ample room for mischief.
Sometimes speed is important. If you are selling flowers or fresh fish or
anything that has to get to market quickly, an auction that takes weeks or
even hours is not a good solution. In some auctions the buyer must be
present, and that is sub-optimal if the auction is in New York and you are in
Tokyo. Different circumstances dictate different answers. Sometimes an auction is useful in hindering dishonest dealings. If the
mayor of New York were free to accept the first bid made by a contractor on a
new city building, the contractor would probably be a relative and the
taxpayers would lose money (again). Are there drawbacks to auctions? Of course. "Winners
curse" is widely recognized as being that phenomenon when a
"lucky" winner pays more for an item than it is worth. Auction
winners are faced with the sudden realization that their valuation of an
object is higher than that of anyone else. In auctions in which no bidder is sure of the worth of the good being
auctioned, the winner is the bidder who made the highest guess. If bidders
have reasonable information about the worth of the item, then the average of
all the guesses is likely to be correct. The winner, however, offered the bid
furthest from the actual value. [Thaler]
(Actually, winner's curse is everywhere in subtle forms. Do you really want
to hire the employee who has been passed over by other employers? Do you want
to be the publisher who buys a manuscript that other editors have rejected?) All in all, the auction, though not always as simple as it appears, can be thought of as a pure marketplace at work in its finest form. ***********************English Auction******************** An important observation
must be made before discussing the various auction formats and that is that
people generally have one of two motivations for participating in an auction
of any type. The first reason is when a bidder wishes to acquire goods for
personal consumption (wine or fresh flowers), and in this case the bidder
makes his own private valuation of the item for sale. All bidders have private
valuations and tend to keep that information private. There would be
little point in an auction if the seller knew already how much the highest
valuation of an object will be. The second reason for bidding in an auction is to acquire items for resale
or commercial use. In this case, an individual bid is predicated not only
upon a private valuation reached independently, but also upon an estimate of
future valuations of later buyers. Each bidder of this type tries (using the
same measurements) to guess the ultimate price of the item. In other words,
the item is really worth the same to all, but the exact amount is unknown.
This is called a common-value
assumption, and one example is that of art purchased solely for promotion in
some secondary market. Purchasing land for its mineral rights is another
example. Each bidder has different information and a different valuation, but
each must guess what price the land might ultimately bring. People's bidding behavior changes depending upon which motivation is
driving them. William Vickrey [Vickrey]
established the basic taxonomy of auctions based upon the order in which
prices are quoted and the manner in which bids are tendered. He established
four major (one sided)
auction types. The English auction is the format most familiar to Americans and is known
also as the open-outcry auction or the ascending-price auction. It is used
commonly to sell art, wine and numerous other goods. Paul Milgrom [Milgrom-1]
defines the English auction in the following way. "Here the auctioneer
begins with the lowest acceptable price--the reserve price-- and proceeds to
solicit successively higher bids from the customers until no one will
increase the bid. The item is 'knocked down' (sold) to the highest
bidder." Contrary to popular belief, not all goods at an auction are actually
knocked down. In some cases, when a reserve price is not met, the item is not
sold. (In other instances discussed later, an item is not really sold because
a shill from the auction house has accidentally bought it.) Some states require
the auctioneer to state at the conclusion of bidding whether or not the item
has been sold. Sometimes the auctioneer will maintain secrecy about the reserve
price, and he must start the bidding without revealing the lowest
acceptable price. One possible explanation for the secrecy is to thwart rings
(subsets of bidders who have banded together and agree not to outbid each
other, thus effectively lowering the winning bid). Despite its seeming simplicity, this auction format is quite complex.
Often bids are not made aloud, but rather signaled--tugging the ear, raising
a bidding paddle, etc. This system of signaling has several advantages.
First, an auction hall would be bedlam if voices were required. Audible bids
increase the likelihood of error because there may be more than one person
bidding at a single instant and an auctioneer cannot be expected to hear them
all. Many traders prefer the semi-anonymity--a known expert in a certain field
may not want others to know he is bidding because it would probably increase
the bidding interest. When a decision to accept signals is made, a system of
price intervals must be introduced so that seller and buyer understand the
signals. In certain situations, an auctioneer has wide discretion. In America
the auctioneer often calls out the amount he has in hand and the amount he is
seeking as well. In England, however, often the auctioneer does not lead
bidders this way, but rather waits to be told what a bidder will offer. Adding to the complexity, competition is at its highest in the English
auction, with some bidders becoming carried away with enthusiasm. Winner's
curse ( paying more for an item than its value) is widespread in this
type of auction because inexperienced participants bid up the price. One variation on the open-outcry auction is the open-exit auction in which
the prices rise continuously, but players must publicly announce that they
are dropping out when the price is too high. Once a bidder has dropped out,
he may not reenter. This variation provides more information about the
valuations (common or public) of others than when players can drop out
secretly (and sometimes even reenter later). In another variation, an auctioneer calls out each asking price and
bidders lift a paddle to indicate a willingness to pay that amount. Then the
auctioneer calls out another price etc. In the ascending-bid format, the auctioneer can exert great influence. He
can manipulate bidders with his voice, his tone, and his personality. He can
increase the pace or even refuse to notice certain bidders (for example, if
he believes someone is a member of a ring, the auctioneer might choose to
ignore him). Eric Rasmusen [Rasmusen]
mentions one unusual variation on the English auction that occurs in France.
After the last bid of an open-cry art auction, a representative of the Louvre
has the right to raise his hand and say, "préemption de l' état"
and take the painting at the highest price. It might be noted that in France,
the auction privilege (the right to conduct an auction ) is sold to a select
few individuals (some 500 throughout the country) by the central government.
This privilege is called the chargé. The key to any successful auction (from a seller's point of view) is the
effect of competition on the potential buyers. In an English auction, the
underbidder usually forces the bid up by one small step at a time. Often a
successful bidder acquires an object for considerably less than his maximum
valuation simply because he need only increase each bid by a small increment.
In other words, the seller does not necessarily receive maximum value, and
other auction types may be superior to the English auction for this reason
(at least from the seller's perspective). [Varian]
Another disadvantage to the English system is that a buyer must be present
which may be difficult and/or expensive. Finally, this auction type is highly
susceptible to rings. ****************Dutch Auction***************** The descending-price
auction, commonly known in academic literature as the Dutch auction, uses an
open format rather than a sealed-bid method. It is the technique used in
Netherlands to auction produce and flowers (hence, a "Dutch"
auction). Unfortunately, the financial world has chosen to refer to another
type of auction as the Dutch auction. In the financial world, the auction
known as "Dutch" is what is referred to in the academic world as a
uniform, second-price auction. Great confusion results. In this series of
articles, the "Dutch" auction will mean a descending-bid structure.
In a Dutch auction, bidding starts at an extremely high price and is
progressively lowered until a buyer claims an item by calling
"mine", or by pressing a button that stops an automatic clock. When
multiple units are auctioned, normally more takers press the button as price
declines. In other words, the first winner takes his prize and pays his price
and later winners pay less. When the goods are exhausted, the bidding is
over. Dutch auctions have been used to finance credit in Rumania and for foreign
exchange in Bolivia, Jamaica, Zambia and have also been used to sell fish in
England and in Israel.
First Price Sealed Bid Auction The third auction type
considered here has a primary characteristic of being sealed (not open-outcry
like the English or Dutch varieties) and thus hidden from other bidders. A
winning bidder pays exactly the amount he bid. Usually, (but not always) each
participant is allowed one bid which means that bid preparation is especially
important. To confuse matters the financial community refers to this type of
auction as an English auction (except in Great Britain where it is known as the
American auction!). In these articles we will use the academic name rather
than that used in financial circles. Speaking generally, a sealed-bid format has two distinct parts--a bidding
period in which participants submit their bids, and a resolution phase in
which the bids are opened and the winner determined (sometimes the winner is
not announced). An important distinction must be made as to quantity--how many goods are
being auctioned--one or multiple items. The name "first-price"
comes from the fact that the award is made at the highest offer when a single
unit is sold. When multiple units are being auctioned, it is called
"discriminatory" because not all winning bidders pay the same
amount. It works like this: In a first-price auction (one unit up for sale) each
bidder submits one bid in ignorance of all other bids. The highest bidder
wins and pays the amount he bid. In a "discriminatory (more than one
unit for sale) auction", sealed bids are sorted from high to low, and
items awarded at highest bid price until the supply is exhausted. The most
important point to remember is that winning bidders can (and usually do) pay
different prices. From a bidder's point of view, a high bid raises the probability of
winning but lowers the profit if the bidder is victorious. A good strategy is
to shade a bid downward closer to market consensus, a strategy that also
helps to avoid winner's
curse. This type of auction is used for refinancing credit and foreign exchange.
Up until 1993, the U.S. Treasury used the discriminatory auction to sell off
its debt, but this method is not without its detractors. In the case of U.S.
Treasury securities, Milton Friedman warned early on that the discriminatory
auction was susceptible to collusion. An investor is reluctant to expose his
valuation to the Treasury because the stated intention of the Treasury is to
gain the highest price possible. It is advantageous to a bidder to gather
information about a competitor's valuation before the auction. Milton
Friedman proved to be prophetic. The U.S. Treasury securities auction will be
discussed later in greater detail.
Vickrey Auction The uniform second-price
auction is commonly called the Vickrey auction, named after William Vickrey,
[Vickrey]
winner of the 1996 Nobel Prize in Economic Sciences, who classified it in the
1960s. Like the first-price auction, the bids are sealed, and each bidder is
ignorant of other bids. (In the financial community, the uniform,
second-price auction is called the Dutch auction, but in these papers we will
use the academic names.) The item is awarded to highest bidder at a price equal to the
second-highest bid (or highest unsuccessful bid). In other words, a winner
pays less than the highest bid. If, for example, bidder A bids $10, bidder B
bids $15, and bidder C offers $20, bidder C would win, however he would only
pay the price of the second-highest bid, namely $15. There is one interesting and crucial point and that is that when
auctioning multiple units, all winning bidders pay for the items at the same
price (the highest losing price). We will see later that the U.S. Treasury
Department is experimenting with this type of auction to sell the national
debt. One wonders why any seller would choose this method to auction goods. It
seems obvious that a seller would make more money by using a first-price
auction, but, in fact, that has been shown to be untrue. Bidders fully
understand the rules and modify their bids as circumstances dictate. In the
case of a Vickrey auction, bidders adjust upward. No one is deterred out of
fear that he will pay too high a price. Aggressive bidders receive sure and
certain awards but pay a price closer to market consensus. The price that
winning bidder pays is determined by competitors' bids alone and does not
depend upon any action the bidder undertakes. Less bid shading occurs because
people don't fear winner's
curse. Bidders are less inclined to compare notes before an auction. This type of auction has been used in former Czechoslovakia to refinance
credit and in Guinea, Nigeria, and Uganda for foreign exchange. What about changing the format just a little and having a second-price,
open-outcry auction? In such a case, participants could bid in the ascending
format and the winner would ultimately pay the price of the second-highest
bid. One might imagine that such an auction would have much the same results
as an English (ascending, open-outcry) auction, but, in fact, an auction like
that would be easy to manipulate. Imagine bidder A bidding $25 for an item
worth $100. Some other bidder could quite easily and safely bid $750, knowing
that no one will bid more and that he will only pay $25. Clearly it is
imperative to seal the bid.
Auction StrategyThe truth is that the
entire subject of auction strategy is numbingly complex with numerous
variables coming into play. Is a bidder risk-averse
or risk-neutral?
Is the auction for one item or multiple units? Do you plan to resell the
acquired object or use it yourself? If you plan to resell it, are the other
bidders symmetric? That is, do they use the same measurements to estimate
their valuations? Do you have secret information about the object? Might
others have secret information? Economists try to devise sets of rules to determine dominant strategies
under a huge array of variables. Bidders, of course, tend to worry more about
their bids than their strategy. From a Seller's Perspective
In any auction a seller
can influence results by revealing information about the object. Intuitively,
a bidder's profits rise when he can exploit information asymmetries (when the
bidder has information not available to others). In general, the more
information a bidder has, the more the price-dampening effect of winner's
curse is lessened. So a seller's optimal strategy is to reveal
information and to link the final price to outside indicators of value (an
authoritative evaluation). It is also a good idea because if a seller seems
reluctant to disclose something, a buyer always assumes the hidden
information must be unfavorable.
(This chart taken from "Going, Going, Gone", by Loretta J.
Mester) [Mester]
But the risk characteristics of a bidder are important too. A bidder who
is risk averse (meaning he absolutely requires the item being auctioned)
tends to bid higher so that he will have a greater chance of victory. A risk
neutral bidder does not.
From a Bidder's Perspective
Theoretical literature
assumes that auction participants are homogeneous (risk neutral and
symmetric--they use the same distribution function to estimate valuations).
It assumes bidders all focus on maximizing profits and that only one item is
being auctioned. English Strategy
In a private-value English
auction, a player's best strategy is to bid a small amount more than the
previous high bid until he reaches his valuation and then stop. This is
optimal because he always wants to buy an object if the price is less than
its value to him, but he wants to pay the lowest possible price. Bidding always
ends when the price reaches the valuation of the player with the
second-highest valuation. Dutch Strategy
The problem for the bidder
in a Dutch auction is exactly the same as that facing a bidder in a
sealed-bid auction. At some point in advance, the bidder must decide the
maximum amount he will bid. He must decide when to stop the auction based
upon his own valuation of the object and his prior beliefs about the
valuations of other bidders. First-Price, Sealed Bid Strategy
It is difficult to specify
a single strategy because a profit-maximizing bid depends upon the actions of
others. The tradeoff is between bidding high and winning more often, and
bidding low and benefiting more if the bid wins (bigger profit margin). Vickrey Strategy
Paul Milgrom [Milgrom
(1)] suggests that the dominant strategy for a bidder in a Vickrey
(second-price) auction is to submit a bid equal to his true reservation
price because he then accepts all offers below his reservation bid and none
that are above. A participant who bids less is more likely to lose the
auction and all that strategy accomplishes is to lower the chance of victory.
Bidding high carries the risk of winner's curse. Neither affects the price
paid if he wins. |
||||||||||||||||||||||||||||||
Cooperative
Games
All of the examples so far have focused on non-cooperative solutions to "games." We recall that there is, in general, no unique answer to the question "what is the rational choice of strategies?" Instead there are at least two possible answers, two possible kinds of "rational" strategies, in non-constant sum games. Often there are more than two "rational solutions," based on different definitions of a "rational solution" to the game. But there are at least two: a "non-cooperative" solution in which each person maximizes his or her own rewards regardless of the results for others, and a "cooperative" solution in which the strategies of the participants are coordinated so as to attain the best result for the whole group. Of course, "best for the whole group" is a tricky concept -- that's one reason why there can be more than two solutions, corresponding to more than concept of "best for the whole group."
Without going into technical details, here is the problem: if people can arrive at a cooperative solution, any non-constant sum game can in principle be converted to a win-win game. How, then, can a non-cooperative outcome of a non-constant sum game be rational? The obvious answer seems to be that it cannot be rational: as Anatole Rapoport argued years ago, the cooperative solution is the only truly rational outcome in a non-constant sum game. Yet we do seem to observe non-cooperative interactions every day, and the "noncooperative solutions" to non-constant sum games often seem to be descriptive of real outcomes. Arms races, street congestion, environmental pollution, the overexploitation of fisheries, inflation, and many other social problems seem to be accurately described by the "noncooperative solutions" of rather simple nonconstant sum games. How can all this irrationality exist in a world of absolutely rational decision makers?
Credible
Commitment
There is a neoclassical answer to that question. The answer has been made explicit mostly in the context of inflation. According to the neoclassical theory, inflation happens when the central bank increases the quantity of money in circulation too fast. Then, the solution to inflation is to slow down or stop increasing in the quantity of money. If the central bank were committed to stopping inflation, and businessmen in general knew that the central bank were committed, then (according to neoclassical economics) inflation could be stopped quickly and without disruption. But, in a political world, it is difficult for a central bank to make this commitment, and businessmen know this. Thus the businessmen have to be convinced that the central bank really is committed -- and that may require a long period of unemployment, sky-high interest rates, recession and business failures. Therefore, the cost of eliminating inflation can be very high -- which makes it all the more difficult for the central bank to make the commitment. The difficulty is that the central bank cannot make a credible commitment to a low-inflation strategy.
Evidently (as seen by neoclassical economics) the interaction between the central bank and businessmen is a non-constant sum game, and recessions are a result of a "noncooperative solution to the game." This can be extended to non-constant sum games in general: noncooperative solutions occur when participants in the game cannot make credible commitments to cooperative strategies. Evidently this is a very common difficulty in many human interactions.
Games in which the participants cannot make commitments to coordinate their strategies are "noncooperative games." The solution to a "noncooperative game" is a "noncooperative solution." In a noncooperative game, the rational person's problem is to answer the question "What is the rational choice of a strategy when other players will try to choose their best responses to my strategy?"
Conversely, games in which the participants can make commitments to coordinate their strategies are "cooperative games," and the solution to a "cooperative game" is a "cooperative solution." In a cooperative game, the rational person's problem is to answer the question, "What strategy choice will lead to the best outcome for all of us in this game?" If that seems excessively idealistic, we should keep in mind that cooperative games typically allow for "side payments," that is, bribes and quid pro quo arrangements so that every one is (might be?) better off. Thus the rational person's problem in the cooperative game is actually a little more complicated than that. The rational person must ask not only "What strategy choice will lead to the best outcome for all of us in this game?" but also "How large a bribe may I reasonably expect for choosing it?"
A
Basic Cooperative Game
Cooperative games are particularly important in economics. Here is an example that may illustrate the reason why. We suppose that Joey has a bicycle. Joey would rather have a game machine than a bicycle, and he could buy a game machine for $80, but Joey doesn't have any money. We express this by saying that Joey values his bicycle at $80. Mikey has $100 and no bicycle, and would rather have a bicycle than anything else he can buy for $100. We express this by saying that Mikey values a bicycle at $100.
The strategies available to Joey and Mikey are to give or to keep. That is, Joey can give his bicycle to Mikey or keep it, and Mikey can give some of this money to Joey or keep it all. it is suggested that Mikey give Joey $90 and that Joey give Mikey the bicycle. This is what we call "exchange." Here are the payoffs:
Table 12-1
|
|
|
Joey |
|
|
|
|
give |
keep |
|
Mikey |
give |
110, 90 |
10, 170 |
|
keep |
200, 0 |
100, 80 |
|
EXPLANATION: At the upper left, Mikey has a bicycle he values at $100, plus $10 extra, while Joey has a game machine he values at $80, plus an extra $10. At the lower left, Mikey has the bicycle he values at $100, plus $100 extra. At the upper left, Joey has a game machine and a bike, each of which he values at $80, plus $10 extra, and Mikey is left with only $10. At the lower right, they simply have what they begin with -- Mikey $100 and Joey a bike.
If we think of this as a noncooperative game, it is much like a Prisoners' Dilemma. To keep is a dominant strategy and keep, keep is a dominant strategy equilibrium. However, give, give makes both better off. Being children, they may distrust one another and fail to make the exchange that will make them better off. But market societies have a range of institutions that allow adults to commit themselves to mutually beneficial transactions. Thus, we would expect a cooperative solution, and we suspect that it would be the one in the upper left. But what cooperative "solution concept" may we use?
Pareto
Optimum
We have observed that both participants in the bike-selling game are better off if they make the transaction. This is the basis for one solution concept in cooperative games.
First, we define a criterion to rank outcomes from the point of view of the group of players as a whole. We can say that one outcome is better than another (upper left better than lower right, e.g) if at least one person is better off and no-one is worse off. This is called the Pareto criterion, after the Italian economist and mechanical engineer, Vilfredo Pareto. If an outcome (such as the upper left) cannot be improved upon, in that sense -- in other words, if no-one can be made better off without making somebody else worse off -- then we say that the outcome is Pareto Optimal, that is, Optimal (cannot be improved upon) in terms of the Pareto Criterion.
If there were a unique Pareto optimal outcome for a cooperative game, that would seem to be a good solution concept. The problem is that there isn't -- in general, there are infinitely many Pareto Optima for any fairly complicated economic "game." In the bike-selling example, every cell in the table except the lower right is Pareto-optimal, and in fact any price between $80 and $100 would give yet another of the (infinitely many) Pareto-Optimal outcomes to this game. All the same, this was the solution criterion that von Neumann and Morgenstern used, and the set of all Pareto-Optimal outcomes is called the "solution set."
Alternative
Solution Concepts
If we are to improve on this concept, we need to solve two problems. One is to narrow down the range of possible solutions to a particular price or, more generally, distribution of the benefits. This is called "the bargaining problem." Second, we still need to generalize cooperative games to more than two participants. There are a number of concepts, including several with interesting results; but here attention will be limited to one. It is the Core, and it builds on the Pareto Optimal solution set, allowing these two problems to solve one another via "competition."
An
Information Technology Example Revisited
When we looked at "Choosing an Information Technology," one of the two introductory examples, we came to the conclusion that it is more complex than the Prisoners' Dilemma in several ways. Unlike the Prisoners' Dilemma, it is a cooperative game, not a noncooperative game. Now let's look at it from that point of view.
When the information system user and supplier get together and work out a deal for an information system, they are forming a coalition in game theory terms. (Here we have been influenced more by political science than economics, it seems!) The first decision will be whether to join the coalition or not. In this example, that's a pretty easy decision. Going it alone, neither the user nor the supplier can be sure of a payoff more than 0. By forming a coalition, both choosing the advanced system, they can get a total payoff of 40 between them. The next question is: how will they divide that 40 between them? How much will the user pay for the system? We need a little more detail about this game before we can go on. The payoff table above was net of the payment. It was derived from the following gross payoffs:
Table A-2
|
|
|
User |
|
|
|
|
Advanced |
Proven |
|
Supplier |
Advanced |
-50,90 |
0,0 |
|
Proven |
0,0 |
-30,40 |
|
The gross payoffs to the supplier are negative, because the production of the information system is a cost item to the supplier, and the benefits to the supplier are the payment they get from the user, minus that cost. For Table A-1, I assumed a payment of 70 for an advanced or 35 for a proven system. But those are not the only possibilities in either case.
How much will be paid? Here are a couple of key points to move us toward an answer:
- The net benefits to the two participants cannot add up to more than 40, since that is the largest net benefit they can produce by working together.
- Since each participant can break even by going it alone, neither will accept a net less than zero.
Using that information, we get Figure A-1:

Figure A-1
The diagram shows the net payoff to the supplier on the horizontal axis and the net payoff to the user on the horizontal axis. Since the supplier will not agree to a payment that leaves her with a loss, only the solid green diagonal line -- corresponding to total payoffs of 40 to the two participants -- will be possible payoffs. But any point on that solid line will satisfy the two points above. In that sense, all the points on the line are possible "solutions" to the cooperative game, and von Neumann and Morgenstern called it the "solution set."
But this "solution set" covers a multitude of sins. How are we to narrow down the range of possible answers? There are several possibilities. The range of possible payments might be influenced, and narrowed, by:
- Competitive pressures from other potential suppliers and users,
- Perceived fairness,
- Bargaining.
There are game-theoretic approaches based on all these approaches, and on combinations of them. Unfortunately, this leads to several different concepts of "solutions" of cooperative games, and they may conflict. One of them -- the core, based on competitive pressures -- will be explored in these pages. We will have to leave the others for another time.
There is one more complication to consider, when we look at the longer run. What if the supplier does not continue to support the information system chosen? What if the supplier invests to support the system in the long run, and the user doesn't continue to use it? In other words, what if the commitments the participants make are limited by opportunism?
Cooperative
Games and the Core
Language
for Cooperative Games
We will need a bit of language to talk about cooperative games with more than two persons. A group of players who commit themselves to coordinate their strategies is called a "coalition." What the members of the coalition get, after all the bribes, side payments, and quids pro quo have cleared, is called an "allocation" or "imputation."
(The problem of coalitions also arises in zero-sum games, if there are more than two players. With three or more players, some of the players may profit by "ganging up" on the rest. For example, in poker, two or more players may cooperate to cheat a third, dividing the pelf between themselves. This is cheating, in poker, because the rules of poker forbid cooperation among the players. For the members of a coalition of this kind, the game becomes a non-zero sum game -- both of the cheaters can win, if they cheat efficiently).
"Allocation" and "imputation" are economic terms, and economists are often concerned with the efficiency of allocations. The standard definition of efficient allocation in economics is "Pareto optimality." Let us pause to recall that concept. In defining an efficient allocation, it is best to proceed by a double-negative. An allocation is inefficient if there is at least one person who can do better, while no other person is worse off. (That makes sense -- if somebody can do better without anyone else being made worse off, then there is an unrealized potential for benefits in the game). Conversely, the allocation is efficient in the Paretian sense if no-one can be made better off without making someone else worse off.
The members of a coalition, C, are a subset of the set of players in the game. (Remember, a "subset" can include all of the players in the game. If the subset is less than the whole set of players in the game, it is called a "proper" subset). If all of the players in the game are members of the coalition, it is called the "grand" coalition. A coalition can also have only a single member. A coalition with just a single member is called a "singleton coalition."
Let us say that the members of coalition C get payoff A. (A is a vector or list of the payoffs to all the members of C, including side payments, if any). Now suppose that some of the members of coalition C could join another coalition, C'; with an allocation of payoffs A'. The members of C who switch to C' may be called "defectors." If the payoffs to defectors in A' are greater than those in A, then we say that A' "dominates" A through coalition C. In other words: an allocation is dominated if some of the members of the coalition can do better for themselves by deserting that coalition for some other coalition.
The
Core
We can now define one important concept of the solution of a cooperative game. The core of a cooperative game consists of all undominated allocations in the game. In other words, the core consists of all allocations with the property that no subgroup within the coalition can do better by deserting the coalition.
Notice that an allocation in the core of a game will always be an efficient allocation. Here, again, the best way to show this is to reason in double-negatives -- that is, to show that an inefficient allocation cannot be in the core. To say that the allocation A is inefficient is to say that a grand coalition can be formed in which at least one person is better off, and no-one worse off, than they are in A. Thus, any inefficient coalition is dominated through the grand coalition.
Now, two very important limitations should be mentioned. The core of a cooperative game may be of any size -- it may have only one allocation, or there may be many allocations in the core (corresponding either to one or many coalitions), and it is also possible that there may not be any allocations in the core at all. What does it mean to say that there are no allocations in the core? It means that there are no stable coalitions -- whatever coalition may be formed, there is some subgroup that can benefit by deserting it. A game with no allocations in the core is called an "empty-core game."
I said that the rational player in a cooperative game must ask "not only 'What strategy choice will lead to the best outcome for all of us in this game?' but also 'How large a bribe may I reasonably expect for choosing it?'" The core concept answers this question as follows" "Don't settle for a smaller bribe than you can get from an other coalition, and don't make any commitments until you are sure."
We will now consider two applications of the concept of the core. The first is a "market game," a game of exchange. We then return to a game we have looked at from the noncooperative viewpoint: the queuing game.
A
Market Game
Economists often claim that "increasing competition" (an increasing number of participants on both sides of the market, demanders and suppliers) limits monopoly power. Our market game is designed to bring out that idea.
The concept of the core, and the effect of "increasing competition" on the core, can be illustrated by a fairly simple numerical example, provided we make some simplifying assumptions. We will assume that there are just two goods: "widgets" and "money." We will also use what I call the benefits hypothesis -- that is, that utility is proportional to money. In other words, we assume that the subjective benefits a person obtains from her or his possessions can be expressed in money terms, as is done in cost-benefit analysis. In a model of this kind, "money" is a stand-in for "all other goods and services." Thus, people derive utility from holding "money," that is, from spending on "all other goods and services," and what we are assuming is that the marginal utility of "all other goods and services" is (near enough) constant, so that we can use equivalent amounts of "money" or "all other goods and services" as a measure of the utility of widgets. Since money is transferable, that is very much like the "transferable utility" conception originally used by Shubik in his discussions of the core.
We will begin with an example in which there are just two persons, Jeff and Adam. At the beginning of the game, Jeff has 5 widgets but no money, and Adam has $22 but no widgets. The benefits functions are
Table 13-1
|
Jeff |
|
Adam |
||||
|
widgets |
benefits |
|
widgets |
benefits |
||
|
|
total |
marginal |
|
|
total |
marginal |
|
1 |
10 |
10 |
|
1 |
9 |
9 |
|
2 |
15 |
5 |
|
2 |
13 |
4 |
|
3 |
18 |
3 |
|
3 |
15 |
2 |
|
4 |
21 |
3 |
|
4 |
16 |
1 |
|
5 |
22 |
1 |
|
5 |
16 |
0 |
Adam's demand curve for widgets will be his marginal benefit curve, while Jeff's supply curve will be the reverse of his marginal benefit curve. These are shown in Figure 13-1.

Figure 13-1
Market equilibrium comes where p=3, Q=2, i.e. Jeff sells Adam 2 widgets for a total payment of $6. The two transactors then have total benefits of
|
|
Jeff |
Adam |
|
widgets |
18 |
13 |
|
money |
6 |
16 |
|
total |
24 |
29 |
The total benefit divided between the two persons is $24+$29=$53.
Now we want to look at this from the point of view of the core. The "strategies' that Jeff and Adam can choose are unilateral transfers -- Jeff can give up 0, 1, 2, 3, 4, or 5 widgets, and Adam can give up from 0-22 dollars. Presumably both would choose "zero" in a noncooperative game. The possible coalitions are a) a grand coalition of both persons, or b) two singleton coalitions in which each person goes it alone. In this case, a cooperative solution might involve a grand coalition of the two players. In fact, a cooperative solution to this game is a coordinated pair of strategies in which Jeff gives up some widgets to Adam and Adam gives up some money to Jeff. (In more ordinary terms, that is, of course, a market transaction). The core will consist of all such coordinated strategies such that a) neither person (singleton coalition) can do better by going it alone, and b) the coalition of the two cannot do better by a different coordination of their strategies. In this game, the core will be a set of transactions each of which fulfills both of those conditions.
Let us illustrate both conditions: First, suppose Jeff offers to sell Adam one widget for $10. But Adam's marginal benefit is only nine -- Adam can do better by going it alone and not buying anything. Thus, "one widget for $10" is not in the core. Second, suppose Jeff proposes to sell Adam one widget for $5. Adam's total benefit would then be 22-5+9=26, Jeff's 5+21=26. Both are better off, with a total benefit of 52. However, they can do better, if Jeff now sells Adam a second widget for $3.50. Adam now has benefits of 13+22-8.50=26.50, and Jeff has benefits of 18+8.50=26.50, for a total benefit of 53. Thus, a sale of just one widget is not in the core. In fact, the core will include only transactions in which exactly two widgets are sold.
We can check for this in the following way. If the "benefits hypothesis" is correct, the only transactions in the core will be transactions that maximize the total benefits for the two persons. When the two person shift from a transaction that does not maximize benefits to one that does, they can divide the increase in benefits among themselves in the form of money, and both be better off -- so a transaction that does not maximize benefits cannot satisfy condition b) above. From Table 13-1,
Table 13-2
|
Quantity Sold |
benefit of widgets |
money |
total |
|
|
|
to Jeff |
to Adam |
|
|
|
0 |
22 |
0 |
22 |
44 |
|
1 |
21 |
9 |
22 |
52 |
|
2 |
18 |
13 |
22 |
53 |
|
3 |
15 |
15 |
22 |
52 |
|
4 |
10 |
16 |
22 |
48 |
|
5 |
0 |
16 |
22 |
38 |
and we see that a trade of 2 maximizes total benefits.
But we have not figured out the price at which the two units will be sold. This is not necessarily the competitive "supply-and-demand" price, since the two traders are both monopolists and one may successfully hold out for a better-than-competitive price.
Here are some examples:
|
Quantity Sold |
Total Payment |
Total Benefits |
|
|
|
|
Jeff's |
Adam's |
|
2 |
12 |
18+12=30 |
22-12+13=22 |
|
2 |
5 |
18+5=23 |
22-5+13=30 |
|
2 |
8 |
18+8=28 |
22-8+13=27 |
What all of these transactions have in common is that the total benefits are maximized -- at 53 -- but the benefits are distributed in very different ways between the two traders. All the same, each trader does no worse than the 22 of benefits he can have without trading at all. Thus each of these transactions is in the core.
It will be clear, then, that there are a wide range of transactions in the core of this two-person game. We may visualize the core in a diagram with the benefits to Jeff on the horizontal axis and benefits to Adam on the vertical axis. The core then is the line segment ab. Algebraically, it is the line BA=53-BJ, where BA means "Adam's benefits" and BJ means "Jeff's benefits," and the line is bounded by BA>=22 and BJ>=22. The competitive equilibrium is at C.

Figure 13-2
The large size of the core is something of a problem. The cooperative solution must be one of the transactions in the core, but which one? In the two-person game, there is just no answer. The "supply-and-demand" approach does give a definite answer, shown as point C in the diagram. According to the supply-and-demand story, this equilibrium comes about because there are many buyers and many sellers. In our example, instead, we have just one of each, a bilateral monopoly. That would seem to be the problem: the core is large because the number of buyers and sellers is small.
So what happens if we allow the number of buyers and sellers to increase until it is very large? To keep things simple, we will continue to suppose that there are just two kinds of people -- jeffs and adams -- but we will consider a sequence of games with 2, 3, ..., 10, ..., 100,... adams and an equal number of jeffs and see what happens to the core of these games as the number of traders gets large.
First, suppose that there are just two jeffs and two adams. Each jeff and each adam has just the same endowment and benefit function as before.
What coalitions are possible in this larger economy? There could be two one-to-one coalitions of a jeff and an adam. Two jeffs or two adams could, in principle, form a coalition; but since they would have nothing to exchange, there would be little point in it. There could also be coalitions of two jeffs and an adam, two adams and a jeff, or a grand coalition of both jeffs and both adams.
We want to show that this bigger game has a smaller core. There are some transactions in the core of the first game that are not in this one.
Here is an example: In the 2-person game, an exchange of 12 dollars for 2 widgets is in the core. But it is not in the core of this game. At an exchange of 12 for 2, each adam gets total benefits of 23, each jeff or 30. Suppose then that a jeff forms a coalition with 2 adams, so that the jeff sells each adam one widget for $7. The jeff gets total benefits of 18+7+7=32, and so is better off. Each adam gets benefits of 15+9=24, and so is better off. This three-person coalition -- which could not have been formed in the two-person game -- "dominates" the 12-for-2 allocation and so the 12-for-2 allocation is not in the core of the 4-person game. (Of course, the other jeff is out in the cold, but that's his look-out -- the three-person coalition are better off. But, in fact, we are not saying that the three-person coalition is in the core either. It probably isn't, since the odd jeff out is likely to make an offer that would dominate this one).
This is illustrated by the diagram in Figure 13-3. Line segment de shows the trade-off between benefits to the jeffs and the adams in a 3-person coalition. It means that, from any point on line segment fb, a shift to a 3-person coalition makes it possible to move to the northwest -- making all members of the coalition better off -- to a point on fe. Thus all of the allocations on fb are dominated, and not in the core of the 4-person game.
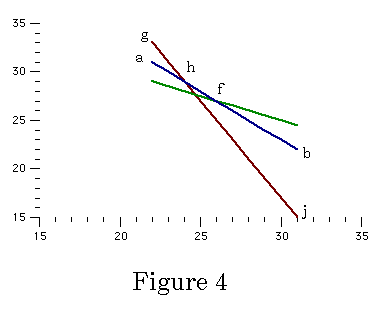
Figure 13-3
Here is another example: in the two-person game, an exchange of two widgets for five dollars is in the core. Again, it will not be in the core of a four-person game. Each jeff gets benefits of 23 and each adam of 30. Now, suppose an adam proposes a coalition with both jeffs. The adam will pay each jeff $2.40 for one widget. The adam then has 30.20 of benefits and so is better off. Each jeff gets 23.40 of benefits and is also better off. Thus the one-adam-and-two-jeffs coalition dominates the 2-for-5 coalition, which is no longer in the core. Figure 13-4 illustrates the situation we now have. The benefit trade-off for a 2-jeff-one-adam coalition is shown by line gj. Every allocation on ab to the left of h is dominated. Putting everything together, we see that allocations on ab to the left of h and to the right of f are dominated by 3-person coalitions, but the 3-person coalitions are dominated by the 2-person coalitions between h and f. (Four-person coalitions function like pairs of two-person coalitions, adding nothing to the game).

Figure 13-4
We can now see the core of the four-person game in Figure 13-4. It is shown by the line segment hf. It is limited by BA>=27, BJ>=24. The core of the four-person game is part of the core of the two-person game, but it is a smaller part, because the four-person game admits of coalitions which cannot be formed in the two-person game. Some of these coalitions dominate some of the coalitions in the core of the smaller game. This illustrates an important point about the core. The bigger the game, the greater the variety of coalitions that can be formed. The more coalitions, often, the smaller the core.
Let us pursue this line of reasoning one more step, considering a six-person game with three jeffs and three adams. We notice that a trade of two widgets for $8 is in the core of the four-person game and we will see that it is not in the core of the 6-person game. Beginning from the 2-for-8 allocation, a coalition of 2 jeffs and 3 adams is proposed, such that each jeff gives up three widgets and each adam buys two, at a price of 3.50 each. The results are shown in Table 13-3
Table 13-3
|
Type |
old allocation |
new allocation |
||||
|
|
widgets |
money |
total benefit |
widgets |
money |
total benefit |
|
Jeff |
4 |
8 |
26 |
3 |
11.4 |
26.4 |
|
Adam |
2 |
14 |
27 |
2 |
14.4 |
27.4 |
We see that both the adams and the jeffs within the coalition are better off, so the two-and-three coalition dominates the two-for-eight bilateral trade. Thus the two-for-eight trade is not in the core of the six-person game.
What is in it? This is shown by Figure 13-5. As before, the line segment ab is the core of the two-person game and line segment gj is the benefits trade-off for the coalition of two jeffs and one adam. Segment kl is the benefits trade-off for the coalition of of two jeffs and thee adams. We see that every point on a, b except point h is dominated, either by a 2-jeff 1-adam coalition or by a two-jeff three-adam coalition. The core of a six-player game is exactly one allocation: the one at point h. And this is the competitive equilibrium! No coalition can do better than it.

Figure 13-5
If we were to look at 8, 10, 100, 1000, or 1,000,000 player games, we would find the same core. This series of examples illustrates a key point about the core of an exchange game: as the number of participants (of each type) increases without limit, the core of the game shrinks down to the competitive equilibrium. This result can be generalized in various ways. First, we should observe that in some games, any game with a finite number of players has more than one allocation in the core. This game has been simplified by only allowing players to trade in whole numbers of widgets. That is one reason why the core shrinks to the competitive equilibrium so soon in our example. We may also eliminate the benefits hypothesis, assuming instead that utility is nontransferable and not proportional to money. We can also allow for more than two kinds of players, and get rid of the "types" assumption completely, at the cost of much greater mathematical complexity. But the general idea is simple enough. With more participants, more kinds of coalitions can form, and some of those coalitions dominate coalitions that could form in smaller games. Thus a bigger game will have a smaller core; in that sense "more competition limits monopoly power." But (in a market game) the supply-and-demand is the one allocation that is always in the core. And this provides us with a new understanding of the unique role of the market equilibrium.
The
Queuing Game and the Core
We have seen that the market game has a non-empty core, but some very important games have empty cores. From the mathematical point of view, this seems to be a difficulty -- the problem has no solution. But from the economic point of view it may be an important diagnostic point. The University of Chicago economist Lester Telser has argued that empty-core games provide a rationale for government regulation of markets. The core is empty because efficient allocations are dominated -- people can defect to coalitions that can promise them more than they can get from an efficient allocation. What government regulation does in such a case is to prohibit some of the coalitions. Ruling out some coalitions by means of regulation may allow an efficient coalition to form and to remain stable -- the coalitions through which it might be dominated are prohibited by regulation.
In another segment, we have looked at a game that has an inefficient noncooperative equilibrium: the queuing game. We shall see that the Queuing Game also is an empty-core game. Recalling that every allocation in the core is Pareto Optimal, and that Pareto Optimality in this game presupposes a grand coalition of all players to refrain from starting a queue, it will suffice to show that the grand coalition is unstable against a defection of a single agent to form a singleton coalition and form a one-person queue.
It is easy to see that the defector will be better off if the rump coalition (the five remaining in a coalition not to queue) continues its strategy of not contesting for any place in line. Then the defector gets a net payoff of 18 with certainty, better than the average payoff of 12.5 she would get with the grand coalition -- and this observation is just a repetition of the argument that the grand coalition is not a Nash equilibrium. But the rump coalition needs not simply continue with its policy of noncontesting. For example, it can contest the first position in line, while continuing the agreement to allocate the balance at random. This would leave the aggressor with a one-sixth chance of the first place, but she can do no worse than second, so her expected payoff would then be (1/6)(18)+(5/6)(15)=15.5. She will not be deterred from defecting by this possible strategy response from the rump coalition.
That is not the only strategy response open to the rump coalition. Table 13-4 presents a range of strategy alternatives available to the rump coalition:
Table 13-4
|
contest the first |
payoff to |
average |
|
no places |
18 |
11 |
|
one place |
15.5 |
11.167 |
|
two places |
13.5 |
11.223 |
|
three places |
12 |
11.2 |
|
four places |
11.167 |
11.167 |
|
five places |
11.167 |
11.167 |
These are not the only strategy options available to the rump coalition. For example, the rump coalition might choose to contest just the first and third positions in line, leaving the second uncontested. But this would serve only to assure the defector of a better outcome than she could otherwise be sure of, making the members of the rump coalition worse off. Thus, the rump coalition will never choose a strategy like that, and it cannot be relevant to the defector's strategy. Conversely, we see that the rump coalition's best response to the defection is to contest the first two positions in line, but no more -- leaving the defector better off as a result of defecting, with an expected payoff of 13.5 rather than 12.5. If follows that the grand coalition is unstable under recontracting.
To illustrate the reasoning that underlies the table, let us compute the payoffs for the case in which the rump coalition contests the first two positions in line, the optimal response. 1) The aggressor has a one/sixth chance of first place in line for a payoff of 18, one/sixth of second place for 15, and four-fifths chance of being third, for 12. (The aggressor must still stand in line to be sure of third place, rather than worse, although that position is uncontested). Thus the expected payoff is 18/6+15/6+4*12/6, for 13.5. 2a) With one chance in six, the aggressor is first, leaving the rump coalition to allocate among themselves rewards of 15 (second place in queue), 14, 11, 8, and 5 (third through last places without standing in the queue). Each of these outcomes has a conditional probability of one-fifth for each of the five individuals in the rump coalition. This accounts for expectations of one in thirty (one-sixth times one-fifth) of each of those rewards. 2b) With one chance in six, the aggressor is second, and the rump coalition allocate among themselves, at random, payoffs of 18 (first place in queue), 14, 11, 8 and 5 (as before) accounting for yet further expectations of one in thirty of each of these rewards. 2c) With four chances in six, the aggressor is third -- without contest -- and the members of the rump coalition allocate among themselves, at random, rewards of 18, 15, (first two places in the queue), 11, 8, and 5 (last three places without queuing). 2d) Thus the expected payoff of a member of the rump coalition is (15+14+11+8+5)/30+(18+14+11+8+5)/30+4*(18+15+11+8+5)/30, or 11.233.
|
|







