First Order logic unification

Home | Unification Algorithm | Terms in Unification | Examples in Unification

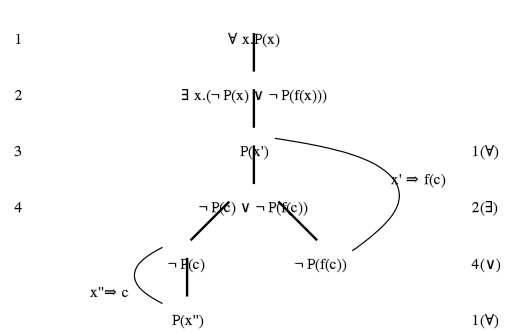
• Let p and q be sentences in first-order logic.

  UNIFY(p,q) = U where subst(U,p) = subst(U,q)

• Where subst(U,p) means the result of applying substitution U on the sentence p. Then U is called a unifier for p and q.
• The unification of p and q is the result of applying U to both of them.
• Let L be a set of sentences, for example, L = {p,q}. A unifier U is called a most general unifier for L if, for all unifiers U' of L, there exists a substitution s such that applying s to the result of applying U to L gives the same result as applying U' to L:

  subst(U',L) = subst(s,subst(U,L))